먼저 말해둘 점은 Godot 3.x 버전이 OpenGL ES를 이용하기 때문에 ray tracing은 지원되지 않는다. 여기서 다룰 내용은 Godot과는 무관하다. 또한, 자세한 수학적 계산은 하지않고 직관적인 내용만 다루고 있다. 수학적 계산이 궁금한 사람은 https://www.scratchapixel.com 를 참고하기 바란다. 3D 렌더링 관련해서 여기만큼 자세하고 수학적인 설명을 하고 있는 웹 문서를 보지 못했다.
Ray Tracing은 가장 현실을 시뮬레이션해서 렌더링하는 알고리즘이다. 만약, 컴퓨터가 ray tracing을 리얼타임으로 구현할 수 있다면, 이 후 다루게 될 수많은 알고리즘들은 몰라도 될 것이다.
현실에서 본다는 것은 눈이나 카메라에 들어오는 빛을 잡아내는 것이다. 빛은 직진을 하므로, 빛이 광원으로부터 눈이나 카메라에 들어오는 경로를 광선으로 표현이 가능하다.
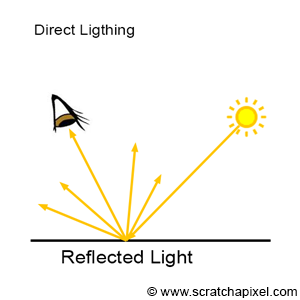
그림처럼, 태양이나 형광등과 같은 광원으로부터 나온 빛이 물체에 반사되어 눈에 들어오게된다. 물체의 표면은 거울과 같은 경우가 아니라면 산란을 일으킨다. 위 그림에서 눈에 들어오는 광선 외에도 밖으로 뻣어나가는 광선들을 표현한 것이 보일 것이다. 실제로는 셀 수 없는 수의 광선들이 뻣어나갈 것이다. 이렇게 산란이 된 광선들은 또 다른 물체에 반사되어 눈에 들어오게 된다. 위 그림은 광원에서 직접 반사된 직접 조명이라면, 이렇게 산란된 광선들이 다시 반사되어 들어오는 것들을 간접 조명이라고 한다.

그림은 단순하게 표현했지만, 현실은 훨씬 복잡하다. 셀 수 없는 광선들이 무한에 가깝게 반사되며 그 결과가 눈에 들어올 것이다.
Ray Tracing은 이 무수한 광선들을 모두 추적하는걸까? 당연히 불가능하다. 현실에 가장 가까운 렌더링 방법이지만, 그대로 흉내내기에는 자연이 너무 어마무시하다. 얘기했던가? 3D computer graphics는 눈속임이라고. 제한된 연산능력으로는 광선의 개수도 좀 적어야 할거 같고, 반사도 조금만 됐으면 좋겠다. 반사가 한 번 일어날 때마다 수많은 광선이 또 나오고 연산은 기하급수적으로 늘어날테니까. 그래서 생각해낸 방법이 광선을 눈으로부터 역추적 하는 방법이다.

직접 조명에 대한 ray tracing은 직관적이고 간단하다. 눈에서 뻣어나간 광선이 반사되어 광원을 향하면 되기 때문이다. 산란된 광선은 신경쓰지 않아도 되니 문제가 단순해진다.
실제로 Ray tracing 알고리즘은 가상의 카메라로부터 화면 스크린의 픽셀단위로 광선을 추적한다. 최종적으로 픽셀의 색을 정하는게 목표이기 때문이다.

만약에 반사된 광선이 광원으로 가지못하고 막힌다면, 그림자로 인식할 수 있다.

문제는 간접 조명이다. 얼마가 될지 모르는 산란되는 광선들을 추적해야 하기 때문이다. 앞에서 힌트를 줬었는데, 3D computer graphics는 눈속임이며, 광선의 개수가 좀 적었으면 좋겠다고 했었다. 그래서 사용되는 방법은 반사면에서 계산 가능한 제한된 개수의 광선을 랜덤한 방향으로 산란시키고, 반사되는 회수도 제한을 두는 것이다. 마치 통계에서 모집단에서 표본을 뽑는 것과 같은 이치이다.

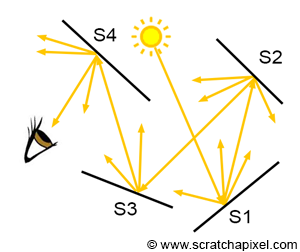
그림과 같이, 랜덤하게 쏘여진 광선들이 물체에 닿게되면, 이들의 칼라를 다 더해 평균을 내서 간접 조명을 계산한다. 이는 컴퓨터로 적분할 때 사용하는 몬테-카를로 기법과 같다.
여러번 반사되는 광선들까지 다루게 된다면 다음과 같은 그림이 될 것이다.

반사 수에 따라서 광선의 수가 기하급수적으로 늘어나고, 반사 지점마다 계산을 해줘야 하므로 계산량이 크게 늘게된다.
이런 몬테 카를로 기법도 단점들이 존재한다. 이는 diffuse object만 시뮬레이션한 것과 같아서, 금속처럼 grossy object의 경우에는 산란이 거의 없으므로 광선을 랜덤하게 분산시키면 안된다.

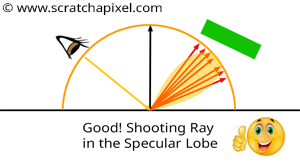
그림을 보면, grossy object의 경우에는 산란이 거의 없다. 광선의 역추적시, 랜덤하게 산란을 시키면 당연하게도 제대로 표현이 되지 않는다. 이런경우 역추적 광선들을 방향성을 갖게 모아줘야한다.
또하나의 단점은 굴절되는 투명 물체의 경우이다.

그림에서 보다시피, ray tracing 기법으로 역추적 하는경우, 실제 광선들을 많이 놓치게 된다.

결과적으로 노이즈가 심한 이미지를 얻게된다. 이런 문제를 해결하기 위해, Photon mapping 이 이용된다. 솔직히, 아직 이게 뭔지 잘 모르겠다. 일단, 이런게 있다는 것만 알고 넘어가자.
이 다음은?
Ray Tracing 기법은 가장 이상적인 렌더링 기법이지만, 실시간으로 적용하기엔 무리가 있다. 최근에 와서 그래픽카드에 RTX가 붙은 것들이 ray tracing을 지원하는 그래픽 카드를 의미한다. 그래서 보통은 정적인 이미지의 렌더링에 사용된다. Blender에서 Cycles rendering이 이에 해당한다. 반면, 게임엔진같은 실시간 렌더링 프로그램들은 Ray Tracing보다 더 많은 속임수를 써서 계산량을 줄인다. 이것들을 알기위해 그 바탕이 되는 Ray Tracing에 대한 기본지식이 필요해서 정리해봤다. 수학적인 내용들을 다 건너띄고 수박 겉핥기라서 찜찜하긴 하지만… 일단, 이런식으로 동작한다는 것 정도만 알고 넘어가자. 이 다음엔, 실시간 렌더링 프로그램들이 어떤 속임수들을 이용해서 이들을 표현하는지 살펴보자.