앞에서 레이 트레이싱에 대해 개념적으로만 간단히 알아봤다. 레이 트레이싱이 현실의 빛을 시뮬레이션 하는 방법이기 때문에, 이론적으로는 가장 명확하고 단순하겠지만, 엄청난 계산량으로 인해 리얼타임 렌더링에서 사용하기엔 제한적이다.
일반적인 리얼타임 렌더링은 두단계로 나뉠 수 있는데, 첫번째로 Geometry Transform들을 통해서 3D 공간의 오브젝트를 스크린 스페이스로 옮겨오면서 어떤 부분들이 보여지는지 판단하는 과정이 필요하고, 두번째로 이렇게 옮겨온 오브젝트를 스크린의 각 픽셀을 무슨색으로 표시할지 Shader를 통해 정하는 단계가 필요하다. 여기에서 다룰 부분은 첫번째 부분인 geometry를 다룰 것이다.
Modeling의 요소
3D 모델링은 보통 3D Max, Maya, Z-brush, Blender와 같은 3D 모델링 툴로 만들어진다. 현실의 오브젝트는 분자, 원자단위로 구성되어 있기 때문에 거시적인 모양을 비슷하게 3D공간에 그려낸다. 여기에서 가장 기본적인 단위로 사용되는 것은 vertex라고 부르는 점들과 이것들로 구성된 선 그리고 삼각형이다. 삼각형을 사용하는 것은 여러 장점이 있는데, 어떤 복잡한 면이든 삼각형을 이어붙여 만들 수 있으면서, 휘어짐이 없는 면의 가장 작은 단위로 여러 수학적인 계산이 단순하다.

OpenGL Transforms
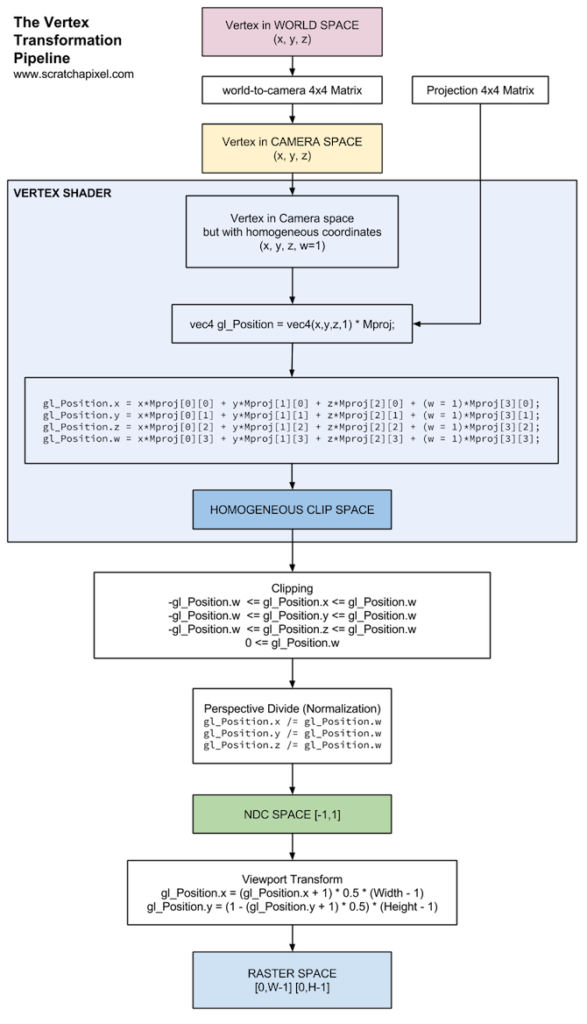
3D공간에 존재하는 모델링 오브젝트들은 변환(Transform)을 거쳐 2D인 모니터 스크린에 그려져야 한다. 대표적인 리얼타임 렌더링 API이며 Godot에서도 사용중인 OpenGL의 경우 다음의 과정을 거친다.

https://learnopengl.com/Getting-started/Coordinate-Systems
Local space는 하나의 오브젝트에 대해 자체적으로 가지는 좌표공간이다. 이렇게 자체적인 좌표공간을 갖는 오브젝트들을 World space라는 공간에 위치시켜 가상세계를 만들어낸다. 여기에서 사용되는 변환이 Model Matrix를 통한 변환(Transform)이며, 스케일, 회전, 이동등을 다룬다.
World Space에는 카메라도 위치하고 있다. 우리가 마치 현실에서 카메라를 통해 세상을 영상에 담듯, 이 가상공간을 가상의 카메라에 담도록 하는 것이다. View Matrix를 이용하여 카메라가 바라보는 방향으로 좌표계를 변환한 공간이 View Space이다.
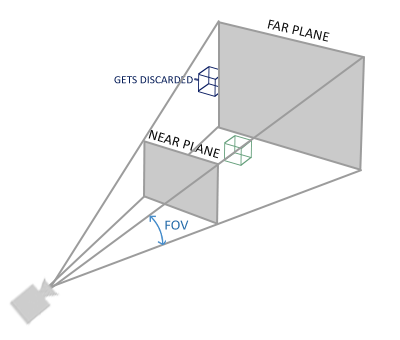
카메라는 화각이 존재하고 카메라를 통해 바라보는 세상은 다음과 같다.
현실의 카메라라면 렌즈 바로 앞에서부터 무한대까지 담아내겠지만, 컴퓨터 그래픽스에서는 제한된 리소스로 인해 화각의 모든 오브젝트들을 담지 않고 제한된 영역의 오브젝트들만 다루기 때문에 near plane/far plane을 지정하고 있다. 이 화면에 보여질 볼륨 영역이 절두체(Frustum)처럼 생겼기 때문에 view Frustum이라 불린다.
이 view frustum을 다음 그림처럼 정육면체 큐브로 압축시킨다.

https://www.scratchapixel.com/lessons/3d-basic-rendering/perspective-and-orthographic-projection-matrix/projection-matrices-what-you-need-to-know-first
이렇게 만들어주는 변환이 Projection Matrix를 통해 이루어진다. 이렇게 큐브로 만들어지면, 큐브를 벗어난 부분들을 잘라내는 Clipping이 이뤄진다.
위 그림에서 보이듯, 클리핑을 하면 삼각형이 아니게 되기 때문에 이를 삼각형으로 쪼개주는 작업이 생긴다. 이렇게 클리핑까지 완료되면, 이제 이 큐브를 x -> [-1, 1], y -> [-1, 1], z -> [-1, 1] 또는 [0, 1]로 정규화(normalize)시킨다. 이렇게 정규화까지 완료된걸 NDC(Normalized Device Coordinates) space라고 부른다. OpenGL에선 이게 Clip space이다.
알아둘 점은 여기까지 아직 Z값이 살아있다는 것이다. 이제 Clip space에서 viewport transform을 통해 2D 스크린 좌표계, screen space로 옮겨온다. screen space의 특징은 제한된 해상도로 인해 rasterize가 필요하다는 점이다. 일반적으로 좌 상단이 원점이되고 오른쪽이 +X축, 아래쪽이 +Y축으로 쓰인다는 것도 주의하자. 또한, 각 픽셀을 그릴때, 가장 가까운 지오메트리만 보여주고 이것보다 멀리있는 것은 가려져야 한다.
해당 픽셀을 그려야할지 가려져서 그리지 말지 결정하는 방법은 다음과 같다. NDC가 직사각형 큐브형태이고 이걸 2D로 옮기는 것은 Orthogonal transform이기 때문에 z값으로 거리를 판단할 수 있다. rasterize를 하며 그리는 과정은 NDC내의 모든 삼각형에 대해 진행된다. 스크린 해상도와 동일한 버퍼를 하나 만들어 두고 최대값으로 초기화한다. 이 버퍼는 z값을 저장하는 depth buffer이다. 삼각형을 rasterize하며 그릴 때, 해당 픽셀의 z값을 이 버퍼의 값과 비교한다. 만약, 버퍼의 값보다 크면 저장하지 않고, 작으면 저장한다. 최대값으로 초기화 되어 있으므로, 처음 그릴 때는 무조건 저장이되며, 모든 삼각형에 대해 처리된 후에는 그중에 최소값만 저장되어 가장 가까운 점들만 남게된다. 이러한 방법을 z-buffering이라고 한다.
이제, 구체적인 변환 매트릭스들에 대해 알아보자. 이를 위해선 Homogeneous Coordinate부터 알아아한다.
Homogeneous Coordinate
Cartesian 좌표계에서 만들어진 3D 모델은 가상의 카메라에 의해 최종적으로 스크린에 그려져야 한다. 우리가 가진 raw 데이타는 3D Cartesian 좌표계의 점들(Vertices)과 이들로 구성되는 삼각형 면들인데, 어떤 변환과정을 거쳐 스크린으로 옮겨오는 것이다. 여기에 사용되는 수학적 도구가 선형대수(Linear Algebra)이다.
일반적으로 생각해보면, 3차원 공간이기 때문에, (x, y, z) 3개 요소를 갖는 벡터와 3X3 매트릭스를 이용하면 될거 같다. 그런데, 3X3 매트릭스는 회전, 스케일변환은 가능하지만, 단순한 이동변환만해도 추가적인게 필요하다. 다르게 말하면, 이동변환(Translation transform)은 선형적인 변환이 아니다. 이를 해결하기 위해서 신기하게도 3차원 벡터에 하나만 더 추가해서 4차원 벡터를 만들면 이동변환 뿐 아니라, 카메라 프로젝션 변환까지 모든게 가능해져 수학적으로 다루기가 매우 편해진다. 이렇게 차용되는 수학적 개념이 Homogeneous Coordinate이다. 이에 대한 수학적 설명은 유튜브 영상 강의(https://www.youtube.com/watch?v=MQdm0Z_gNcw) 를 참고하자. 찾아본 것중에 설명이 가장 깔끔하고 좋았다.
3차원에 대한 Homogeneous Coordinate는 하나를 추가한 4차원이다. 여기서 벡터는 다음과 같이 정의 된다.
\begin{bmatrix}
x \\
y \\
z \\
w
\end{bmatrix}
= \lambda
\begin{bmatrix}
x \\
y \\
z \\
w
\end{bmatrix}
, \lambda \not = 0, \vert \bold x \vert = x^2 + y^2 + z^2 + w^2 \not = 0즉, 0을 제외한 스칼라 값을 곱해도 다 동일한 값이다. 이걸 어떻게 3D 변환에 사용할까? 이 homogeneous Coordinate는 우리가 유클리드 기하학에서 사용하는 3차원 Cartesian Coordinate를 포함하고 있다. 바로 w = 1인 경우가 이에 해당한다. 스칼라 값을 곱해도 변하지 않는 성질을 이용해서 Cartesian Coordinate와 Homogeneous Coordinate간 변환이 가능하다. 바로 w로 각 엘리먼트를 나눠주면 된다.
\begin{bmatrix}
x \\
y \\
z \\
w
\end{bmatrix} =
\begin{bmatrix}
x/w \\
y/w \\
z/w \\
1
\end{bmatrix}그런데, 특수한 경우가 생긴다. w = 0이면 불가능하지 않나? 이경우 Homogeneous Coordinate에서는 무한대로 정의한다. w가 0으로 수렴하는 limit의 개념으로 생각해보면 이해를 도울 수 있을 것이다. 흥미로운 부분인데 infinity point를 유한한 값으로 표시가 가능해진 것이다. x, y, z가 무한대로 간다는 얘기는 기하학적으로는 point를 말한다기보다 방향(direction)만 표현하고 있다고 볼 수도 있다. 실제로 이런 개념으로 사용된다.
TMI하나. 2D에서 다루게되면, Homogeneous Coordinate는 w가 z축에 해당하는 3차원에서 z = 1인 2차원으로 Perspective Projection 하는 것에 해당한다. 프로젝션을 계산해보면, 거리에 반비례한 x/z, y/z 값으로 매핑이 되기 때문이다. 이건 3D공간에서 카메라를 이용해 사진촬영을 했을 때 보이는 모습과 같다. 잼있는걸 하나 더 말하자면, 열차 철로를 사진으로 찍는다면 3D에서 평행한 열차철로가 사진속에서는 한 점에서 만나게된다. 두 라인의 교차점을 계산해보면, 이 만나는 점이 Homogeneous Coordinate에서는 w = z = 0인 무한대 값이 된다. 계산 방법은 호기심이 있다면 찾아보길 🙂
Basic Transforms
Homogeneous Coordinate를 사용하면, 간단하게 4X4 매트릭스를 이용해 각종 기하변환들을 수행할 수 있다.
Scale
\begin{bmatrix}
x' \\
y' \\
z' \\
1
\end{bmatrix} =
\begin{bmatrix}
S\scriptstyle{x} & 0 & 0 & 0 \\
0 & S\scriptstyle{y} & 0 & 0 \\
0 & 0 & S\scriptstyle{z} & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}스케일 매트릭스는 직관적이다. x’ = S_x * x 와 같은 연산으로 각 좌표축에 대해 크기만 변경시킨다.
Translation
이동변환은 간단하지만 3X3 매트릭스로 표현이 안되므로, Homogeneous Coordinate를 쓰는 이유중에 하나가 된다. 매트릭스는 다음과 같다.
\begin{bmatrix}
x' \\
y' \\
z' \\
1
\end{bmatrix} =
\begin{bmatrix}
0 & 0 & 0 & T_x \\
0 & 0 & 0 & T_y \\
0 & 0 & 0 & T_z \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}계산을 해보면, x’ = x + Tx 와 같은 형태로 translation이 되는걸 확인할 수 있다.
Rotation
로테이션의 가장 간단한 형태는 X, Y, Z 각 축에 대한 회전이다. 예를 들면, Z축에 대한 회전이라면 2D 회전과 동일하다. 각 축에대한 회전을 Homogeneous Coordinate 폼을 이용해서 써보면 다음과 같다. ( LearnOpenGL 사이트 참조 )
X-axis rotation
\begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & cos\theta & -sin\theta & 0 \\
0 & sin\theta & cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}Y-axis rotation
\begin{bmatrix}
cos\theta & 0 & sin\theta & 0 \\
0 & 1 & 0 & 0 \\
-sin\theta & 0 & cos\theta & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}Z-axis rotation
\begin{bmatrix}
cos\theta & -sin\theta & 0 & 0 \\
sin\theta & cos\theta & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}2D에서 회전식은 중고등학생 때 배웠던 내용일텐데, 잘 기억이 안난다면 https://matthew-brett.github.io/teaching/rotation_2d.html 를 참고하면 된다.
임의의 회전(Arbitrary rotation)
좌표계의 임의의 회전상태를 이 고정된 x, y, z축의 회전으로 나타내는걸 오일러각(Euler angle)이라고 한다. 이것은 앞에서 각 x, y, z축에 대한 회전 매트릭스의 곱으로 표현할 수 있다. 문제는 하나의 축에 대해 회전을 시키면, 다른 축이 같이 돌아간다는 점이다. 아래 애니메이션으로 확인해보자.

애니메이션을 잘 보면, z축에 대해 회전 -> 변경된 x축에 대해 회전 -> 변경된 z축에 대해 회전 순서로 돌아간다.

이 회전 매트릭스를 표현하면 다음과 같이 된다.
\bold{R} = \bold{R}_z(\alpha) \bold{R}_{x'}(\beta)\bold{R}_{z''}(\gamma)여기서는 z-x’-z” 순으로 회전시켰지만, 회전 순서에 따라 여러 조합이 가능하다. 각(angle) 파라미터가 달라 지겠지만, 좀 더 익숙하게 x-y’-z” 같은 조합도 된다.
문제는 임의 축을 중심으로한 회전을 다루기가 어렵고, 엔지니어링 측면에서 gimball lock이라는 현상이 생긴다는 점이다. 이는 쿼터니언(Quaternian)을 사용하면 모든게 해결된다. 쿼터니언은 허수를 포함한 4차원 공간이다.
q = a + b\bold{i} + c\bold{j} + d\bold{k}, \\
\space \\
\bold{i}, \bold{j}, \bold{k} \text{ are unit vector in imagenary space,} \\
\space \\
\bold{i}^2 = \bold{j}^2 = \bold{k}^2 = -1 \\
\bold{i}\bold{j} = \bold{k},\space \bold{j}\bold{i} = -\bold{k} \\
\bold{j}\bold{k} = \bold{i},\space \bold{k}\bold{j} = -\bold{i} \\
\bold{k}\bold{i} = \bold{j},\space \bold{i}\bold{k} = -\bold{j}
3차원 공간상의 벡터를 쿼터니언 공간으로 변환하면 실수부분이 0인 값으로 표현한다.
\bold{v} = (x, y, z) \rightarrow \bold{q} = (x, y, z, 0) = x\bold{i} + y\bold{j} + z\bold{k}흥미로운 부분은 임의 방향을 중심으로하는 회전을 쿼터니언이 표현할 수 있다는 점이다. 특정 방향을 가리키는 단위벡터를 u라고 한다면, 다음과 같이 쓸 수 있다.
\bold{u} = u_x \bold{i} + u_y \bold{j} + u_z \bold{k} \\
\bold{q} = cos{{\theta}\over{2}} + sin{{\theta}\over{2}}(u_x \bold{i} + u_y \bold{j} + u_z \bold{k}) = cos{{\theta}\over{2}} + sin{{\theta}\over{2}}\bold{u}쿼터니언을 이용한 회전에 대해 수학적으로 정리하자면 어렵고 내용이 많다. 아마도 새로운 포스팅 하나가 필요할 것이다. 위키피디아 쿼터니언 회전에 대해 정리된게 있고 그외에도 구글링을 해보면 많은 자료를 찾을 수 있으니 여기서는 생략하고 간단하게 결과만 이용하겠다.
위에서 보여준 회전에 대한 쿼터니언 q를 사용하면, 벡터 p의 회전은 다음과 같이 계산된다.
\bold{p'} = \bold{q(\theta)}\bold{p}\bold{q'(\bold{\theta})}자세한 설명은 생략했으나, 설명된 euclidianspace 사이트를 참조하면 다음 그림처럼 도식화 할 수 있다.

계산 결과만 이용하면, 쿼터니언을 이용했을 때, 다음과 같이 매트릭스 폼으로 표현이 된다.
\bold{R} = \begin{bmatrix}
1-2({q_j}^2+{q_k}^2) & 2({q_i}{q_j} - {q_k}{q_r}) & 2({q_i}{q_k} + {q_j}{q_r}) \\
2({q_i}{q_j} + {q_k}{q_r}) & 1-2({q_i}^2+{q_k}^2) & 2({q_j}{q_k} - {q_i}{q_r}) \\
2({q_i}{q_k} - {q_j}{q_r}) & 2({q_j}{q_k} + {q_i}{q_r}) & 1-2({q_i}^2+{q_j}^2) \\
\end{bmatrix} ,\\
\space \\
\bold{q} = {q_r} + {q_i}\bold{i} + {q_j}\bold{j} + {q_k}\bold{k}, \\앞에서 봤듯이, qi, qj, qk, qr들은 회전각과 방향벡터의 성분값에 의존한다. 이 두개를 결합하면, 회전 매트릭스를 방향벡터와 회전각으로 표현이 된다. 결과 매트릭스가 3X3이므로 이걸 homogeneous coordinate인 4X4로 표시하면 다음과 같다.
\bold{R} = \\
\begin{bmatrix}
cos\theta + {u_x}^2(1−cos\theta) & {u_x}{u_y}(1 - cos\theta) - {u_z}sin\theta & {u_x}{u_z}(1 - cos\theta) + {u_y}sin\theta & 0 \\
{u_y}{u_x}(1 - cos\theta) + {u_z}sin\theta & cos\theta + {u_y}^2(1−cos\theta) & {u_y}{u_z}(1 - cos\theta) - {u_x}sin\theta & 0\\
{u_z}{u_x}(1 - cos\theta) - {u_y}sin\theta & {u_z}{u_y}(1 - cos\theta) + {u_x}sin\theta & cos\theta + {u_z}^2(1−cos\theta) & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}Rotation Interpolation : SLERP(Spherical Linear Interpolation)
쿼터니언을 쓰는 또하나의 이유는 바로 애니메이션에 사용되는 회전 보간법 때문이다. 지오메트리 또는 오브젝트가 임의의 회전을 할 때, 오일러 앵글을 따라 회전을 하면 앞에서 봤던 오일러 앵글 애니메이션처럼 이상하게 보일 것이다. 일단, 보간에 사용되는 파라미터가 3개의 각도가 필요하기 때문에 곤란하다. 쿼터니언을 쓰면 각도에 대한 파라미터가 하나이므로 이게 가능해진다. 여기에 사용되는 것이 SLERP 이다.
먼저 더 단순한 선형 보간법인 LERP를 알아보자. qa 쿼터니언에서 qb로의 회전을 생각하면 다음과 같이 두 쿼터니언간 선형 보간이 가능하다.
\bold{q_{int}} = t\bold{q_a} + (1-t)\bold{q_b}, \space 0 \le t \le 1위의 선형 보간을 도식화 해보면, 두 쿼터니언을 연결하는 직선이 되고, 아래 그림에서 왼쪽에 해당한다.
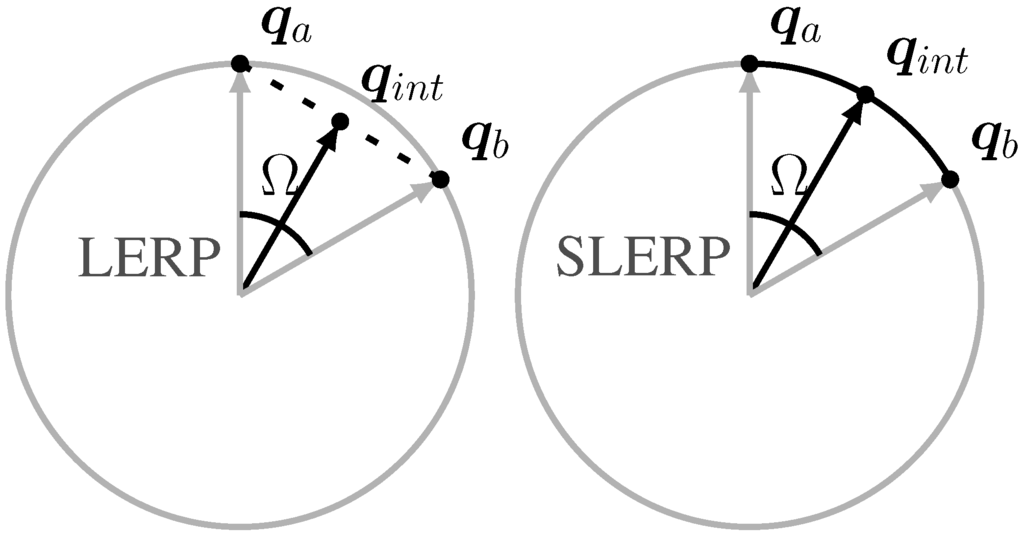
우리가 원하는건, 위 그림에서 오른쪽처럼 구면을 따라 움직이는 보간법이다. 이게 앞에서 말한 SLERP이다.
SLERP를 유도하기 위해, 다음 그림을 보자.
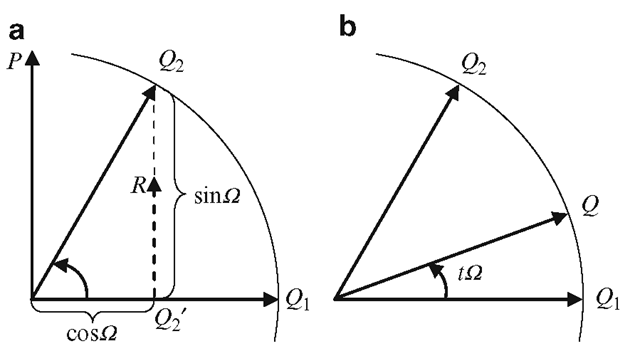
http://what-when-how.com/advanced-methods-in-computer-graphics/quaternions-advanced-methods-in-computer-graphics-part-5/
P는 Q1과 직교하는 쿼터니언이고, Q1, Q, Q2, P 모두 유닛 쿼터니언이다. P는 쿼터니언 R의 크기가 1이 될 때 같아진다. R방향 쿼터니언은 Q2 – Q2’으로 쓸수 있고, Q2′ = Q1cosΩ 이므로 다음과 같이 쓸 수 있다.
\bold{P} = {Q_2 - Q_1 cos\Omega \over sin{\Omega}}sinΩ 로 나눠준 것은 Q2 – Q2’의 크기가 sinΩ이므로 크기를 1로 만들어 주기 위함이다.
위 그림의 오른쪽 b그림을 보면, 파라미터 t를 사용한 보간값 쿼터니언 Q를 다음과 같이 쓸 수 있다.
\bold{Q} = cos(t\Omega)\bold{Q_1} + sin(t\Omega)\bold{P},\space 0 \le t \le 1Q1, P를 직교하는 좌표처럼 사용한 표현이다. (쿼터니언이지만 벡터라고 생각하면 직관적으로 이해할 수 있다.) Q의 크기가 1이므로, Q1에 사영한 값은 cos(tΩ)이고, P에 사영한 값은 sin(tΩ)이다.
이제 이 두 식에서 P를 제거해보면, Q는 다음과 같이 쓰인다.
\bold{Q}(t) = {sin((1-t)\Omega)\bold{Q_1} + sin(t\Omega)\bold{Q_2} \over sin(\Omega)}\\
\space \\
0 \le t \le 1이 식을 이용하면 Q1에서 Q2로 가는 회전에서 매개변수 t를 이용하여 보간 쿼터니언 Q(t)를 얻을 수 있다.
Perspective Projection
perspective projection은 view frustum을 near plane 크기의 정육면체로 바꾸는 변환이다. 이후에 정규화까지 하게되면 NDC가되어 다음 그림의 왼쪽에서 오른쪽이 된다.

http://www.songho.ca/opengl/gl_projectionmatrix.html
위 그림에서 왼쪽 그림을 보면, 좌표계는 가장 보편적인 오른손 좌표계가 사용되고, 이 경우 XY plane을 바라보는 카메라 또는 눈은 -Z 방향을 바라보고 있게 된다. 반면, 변환 결과물인 오른쪽을 보면, Z방향이 플립되어 왼손 좌표계가 사용된다. 이렇게 쓰는 이유는, 왼쪽 frustum안의 모든 Z값은 마이너스가 되는데, 계산과정에서 필요한건 Z방향의 거리이므로 항상 플러스인게 간편해지기 때문이다. 즉, 변환의 시작은 Z축을 뒤집는 것에서 시작한다.
z' = -z
하나의 점에 대해 Y축 perspective projection을 생각해보자.

view frustum안의 점 P를 Z=d 인 위치에 있는 near plane상에 매핑해 새로운 점 P’을 구하는 것이다. 삼각형의 비율을 이용하면,
\overline{BP}:\overline{AP'} = \overline{OB}:\overline{OA} \\
\overline{AP'}\space \overline{OB} = \overline{BP} \space \overline{OA} \\
\overline{AP'} = {\overline{BP} \space \overline{OA} \over \overline{OB}} \\
좌표를 이용해 표현하면 다음과 같이 된다.
\overline{OA} = d = n(\text{near plane}), \overline{AP'} = y', \overline{BP} = y\\
\space \\
y' = {ny \over -z} x도 마찬가지 이므로, x’, y’, z’을 다 정리하면,
x' = {nx \over -z} , \space y' = {ny \over -z}, \space z' = nx’ ,y’ 이 z 의존성을 갖고 있다는 점을 주의깊게 봐야한다. 여기서 homogeneous coordinate의 특징을 사용해 w’값을 이용해보자. 앞에서 다뤘듯, homogeneous coordinate 벡터는 어떤 값을 곱해도 같은 값이고, w’이 1이 아닐 때 cartesian coordinate로 변환하려면 w’으로 나눠줘서 1로 만들어 줬었다. 그렇다면, x’ = dx 가되고, w’ = -z 가되면, 다음과 같이 원하는 결과와 일치한다.
\begin{bmatrix}
x' \\
y' \\
z' \\
w'
\end{bmatrix} =
\begin{bmatrix}
nx \\
ny \\
-nz \\
-z
\end{bmatrix} =
\begin{bmatrix}
-nx/z \\
-ny/z \\
n \\
1
\end{bmatrix}
이걸 만족시키도록 매트릭스를 적어보면 다음과 같다.
\begin{bmatrix}
x' \\
y' \\
z' \\
w'
\end{bmatrix} =
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0 \\
0 & 0 & -n & 0 \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}w’ = -z를 만들어 주는게 x’, y’이 z에 대한 의존성을 갖는 비선형 변환에 대한 키가 되는 것이다.
프로젝션 매트릭스를 구하긴 했는데, 이는 사실, near plane상의 값들이다. 어쨌든, z에 대한 데이터를 상실해버리는건 문제다. z’값을 상수가 아닌 원래 z의 크기값을 갖도록 해야하는데, 하는김에 normalize 시킨 NDC로 변환을 시키도록 하자. 이렇게 하는 이유는 OpenGL의 clipping space가 NDC이기 때문에, OpenGL에서 사용하는 Projection matrix가 위에서 설명한 projection과 동시에 NDC에 맞게 변환 시키는 매트릭스이기 때문이다.
먼저 z’에 대해서만 다룬다면 다음과 같이 쓸 수 있다.
\begin{bmatrix}
x' \\
y' \\
z' \\
w'
\end{bmatrix} =
\begin{bmatrix}
n & 0 & 0 & 0\\
0 & n & 0 & 0 \\
0 & 0 & m_{22} & m_{23} \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}z’이 x, y 의존도는 없기 때문에, m00 = m11 = 0으로 쓸 수 있고, m22, m23 두 엘리먼트에 의해 결정이 된다.
NDC는 z범위가 [-1, 1]이기 때문에, z = -n(near plane) 일 때, z’/w’ = -1이 된다. z = -f(far plane)일 때, z’/w’ = 1이 된다. 이걸 이용해 연립방정식을 풀 수 있다.
z' = m_{22}z + m_{23} \\
{z' \over w'} = {z' \over -z} ,\space w' = -z \\
{-m_{22}n + m_{23} \over n} = -1, z = -n \\
\space \\
{-m_{22}f + m_{23} \over f} = 1, z = -f
\space \\
\therefore m_{22} = -{f+n \over f - n}, \\
\space \\
\space\space\space m_{23} = -{2fn \over f-n}
매트릭스는 다음과 같이 쓸 수 있다.
\begin{bmatrix}
x' \\
y' \\
z' \\
w'
\end{bmatrix} =
\begin{bmatrix}
n & 0 & 0 & 0\\
0 &n & 0 & 0 \\
0 & 0 & -{f+n \over f - n} & -{2fn \over f-n} \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}x, y에 대해서도 NDC를 적용해 계산해보자. xp 가 [l, r]의 범위라고 할 때, normaize된 xn 은 [-1, 1] 범위를 갖는다. 이러한 매핑을 그래프로 그려보면 다음과 같다.

http://www.songho.ca/opengl/gl_projectionmatrix.html
직선의 방정식을 이용해서 표현해보면,
x_n = {1-(-1) \over r - l}x_p + c_xcx 는 상수이다. 이 직선은 (r, 1)을 지나가므로 값을 입력해보면 상수를 구할 수 있다.
1 = {2 \over r-l}r + c_x,\\
c_x = 1- {2r \over r-l} \\
\space \\
=-{r + l \over r-l}이를 다시 직선의 방정식에 대입하면,
x_n = {2 \over r - l}x_p - {r+l \over r-l}y에 대해서도 동일한데, left/right 대신 top/bottom으로 t, b를 써서 표현하면,
y_n = {2 \over t - b}y_p - {t+b \over t-b}이 식들은 단순히 [-1, 1]로 매핑하는 공식이다. xp , yp 에 x’, y’을 대입하면 다음과 같이 정리된다.
x_n = {2 \over r-l}({nx \over -z}) - {r+l \over r-l}\\
\space \\
= ({2n \over r-l}x + {r+l \over r-l}z){1 \over -z}
\space \\
\space \\
y_n = ({2n \over t-b}y + {t+b \over t-b}z){1 \over -z}w’이 -z이고 이 값으로 나눠지는걸 생각해보면, 위 식에서 1/(-z) 부분은 이에 대한 표현으로 생각할 수 있다. 그렇다면, 매트릭스에서는 그 앞의 식만 고려하면 된다.
\begin{bmatrix}
x' \\
y' \\
z' \\
w'
\end{bmatrix} =
\begin{bmatrix}
{2n \over r - l} & 0 & {r+l \over r-l} & 0\\
0 & {2n \over t - b} & {t+b \over t-b} & 0 \\
0 & 0 & -{f+n \over f - n} & -{2fn \over f-n} \\
0 & 0 & -1 & 0
\end{bmatrix}
\begin{bmatrix}
x \\
y \\
z \\
1
\end{bmatrix}매트릭스를 풀어쓰면, 앞에서 유도한 식이 나옴을 검산해볼 수 있을 것이다.
NDC로 normalize 시키면서 x’, y’에 z값에 대한 의존도가 추가되었다. 이는 l(left), r(right), t(top), b(bottom) 바운더리를 두면서 고정된 n(near plane) 위치에 이 바운더리에 따라 projection이 달라진다는 얘기이다. 이는 시야각에 대한 내용이며, 바운더리 l, r, t, b과 n값을 이용해 폭(width)와 넓이(height)에 대한 각각의 시야각(Field of view)을 각도로 계산할 수 있다.
OpenGL에서 클리핑은 이 프로젝션 매트릭스를 곱한 결과값에서 계산된다. w’으로 나눠지기 전에는 아직 normalized 되지 않은 homogeneous coordinate상의 포인트이다. w’으로 나눠졌을 때, NDC space가 되어 [-1, 1]의 범위를 갖게되므로, 나누기 전에는 x’, y’, z’ 모두 [-w’, w’]의 동일한 범위를 갖게 된다. 그러므로 클리핑 계산이 간단하다. 이는 OpenGL 파이프라인을 설명하는 다음 그림에서 보다 직관적으로 이해 가능하다.
Viewport Transform
이제 NDC space의 점들을 스크린의 뷰포트로 옮겨야 한다.

스크린은 좌상단을 (0,0)으로 갖고 있으며, 우측으로 X축, 아래로 Y축이 증가한다. 스크린상 윈도우가 뷰포트(viewport)이며, 그 위치를 (x0,y0)라고 하자. x0는 NDC의 -1에 해당하고 (x0 +w)은 NDC의 1에 해당한다. 마찬가지로 y0는 -1, (y0+h) 는 1에 해당한다. NDC상의 점 (xn, yn)이라고 한다면, 뷰포트상의 점 (x, y)는 다음과 같이 구해진다.
x_n - (-1) : x - x_0 = 1 - (-1) : w \\
2(x - x_0) = w(x_n + 1) \\
\space \\
x = {w \over 2}x_n + (x_0 + {w \over 2})
마찬가지로 y에 적용하면,
y = {h \over 2}y_n + (y_0 + {h \over 2})흥미로운 점은 뷰포트에서도 z값을 버리지 않고 사용한다. z축으로 가까운 위치를 n(near), 먼 위치를 f(far)로 표시한다면, 각각 -1, 1에 해당한다. x, y의 계산법과 동일하게 해보면,
z = {(f-n) \over 2}z_n + (n + {f-n \over 2}) \\
\space \\
= {(f-n) \over 2}z_n + {(f + n) \over 2}다 합쳐보면, 다음과 같다.
x = {w \over 2}x_n + (x_0 + {w \over 2}) \\
\space \\
y = {h \over 2}y_n + (y_0 + {h \over 2}) \\
\space \\
z= {(f-n) \over 2}z_n + {(f + n) \over 2}마무리
공부하면서 오랜기간에 걸쳐 작성한 포스팅이라서 좀 일관성이 없어 보이기도 한다. 이 포스팅만으로 학습하기엔 구멍이 숭숭 뚫린게 보이지만, 필요한 개념들은 짚고 넘어갔기 때문에 적어도 나에게는 기억을 되살리고 관련된 학습과정에 도움이 되긴 할거 같다. 아뭏튼… 잘 몰라서 힘들었다 ㅋㅋㅋㅋ 이렇게 어렵게 적었는데도, 쿼터니언 관련해서는 언젠가 추가적인 정리가 필요하겠지. 처음 공부라 가능하면 수학적으로 정리했는데, 뭐 사실… 컴터와 API가 다 해준다. 사용하는게 어렵지는 않을거란 얘기.
Godot으로는 카메라 노드에 대한건 좀 다뤄야 하긴 하는데, 내 모든 에너지가 방전되어 버렸다. 위 내용을 기반으로 카메라 노드 문서를 참고하시라. 이렇게 말했지만, 언젠간 추가해야할 내용…
이제 본격적으로 쉐이더 부분을 먼저 파보도록 하겠다. 관련해서는 Godot에서도 만질게 많을 거 같네.